ニューラルネットの調和解析
はじめに
この記事はDeep Learning Advent Calendar 2016 3日目の記事です.
とうとうAdventCalendar以外でブログを更新しなくなってしまいましたが,元気よく書いていきたいと思います.
今回はニューラルネットのブラックボックス性とその解析をしている論文の紹介です.Deep Learning Advent Calendarをやるぞ!と言っておきながら,この記事で取り上げるのは浅いニューラルネットです.
ニューラルネットのブラックボックス性とその議論
ニューラルネットは自然言語処理や音声認識,ゲームAIなどの様々なタスクに応用されるようになり,いずれも大きな成果を挙げていることに間違いはありません.
しかしその一方で,ニューラルネットは中間層を挟むため,学習で得られる内部状態は不明瞭となります.このことから,結果の考察がしにくいという理由で忌避されることも多いと思います*1.
この問題は1980年代後半から議論されています.議論は中間層の素子数と目的関数の近似誤差の関係に着目するという方向性となり,"基底となる関数を自由に選べるという条件下で,中間層素子が無限にあれば任意の関数を近似できる"という命題のもと,様々な証明のテクニックが考案されました.Irie, Miyake, Cybenko,Whiteらは,フーリエスライス定理やラドン変換などの概念に基づいて,この命題を証明しています[1, 2, 3].Funahashiはまた,Kolmogorov-Arnoldの定理とSprecherの定理を使って証明を与えています[4].
この議論を進めていくうちに,Anzellottiは,目的関数のクラスを限ると,3層ネットワークの平均二乗誤差の上限は中間層の数に反比例することを示しました[5].それは多層ネットワークと勾配降下法を用いた手法が,次元の呪い*2に束縛されないことを意味しています.
1996年にMurata[6],1998年にはCandes[7]が,ニューラルネットの非線形変換に適したRidge関数を用いて,Ridge関数の積分変換と逆変換を定義し,この積分表現(後述します)を利用することで,Murataらは単純な3層ネットワークの中間層の素子に直接的な意味を与えられることを示しました. このアイデアは,3層ネットワークの関数近似の問題を過完備基底関数系上での展開と捉え.その近似性能を論じたものです.
積分表現はニューラルネットを関数解析的に扱えるという大きなメリットがあります.この積分表現について,少しだけ触れていきたいと思います.
まずはRidge関数の積分表現です.
Ridge関数を用いた積分表現
Ridege関数の積分表現は以下のリンク先で書いたので,こちらを参照して頂きたいと思います.
MurataはこのRidge関数の積分変換を3層ネットワークに取り入れることで,中間素子数nの3層ネットワークの平均二乗誤差がオーダ1/n以下で近似できると定量的に示しました.
その後,Sonodaらはこの理論を発展させ,活性化関数の新しいデファクトスタンダードであるRectified Linear Unit (ReLU)を用いた場合でも,3層ネットワークが上記で示した万能近似性能を有していることを示しています[8].
ニューラルネットの積分表現
活性関数ηを持つニューラルネット(3層ネットワーク)の関数 \( f : \mathbb{R}^m → \mathbb{C} \)の近似を以下のように定義します.
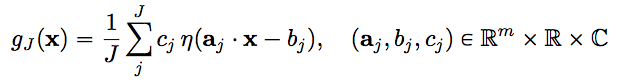
この時,\( (a_j, b_j) \) は中間層(hidden layer)のパラメータで,\( c_j \)は出力層のパラメータです. このニューラルネット\( g_J(x) \)は,以下のニューラルネットの積分表現を離散化することによって得ることができます.
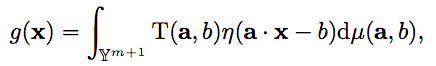
ニューラルネットの和の部分を積分に置き換え,連続化した関数を得ることを積分表現といいます.
\( \mathbb{Y}^{m+1} \) は中間層のパラメータ空間 \( \mathbb{R}^m \times \mathbb{R} \)です.右辺は,ηに対するT(a, b)の双対リッジレット変換とされています.
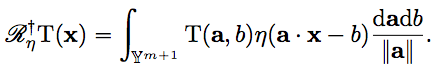
T(a,b)において,Ψに関するfのリッジレット変換を代入することによって
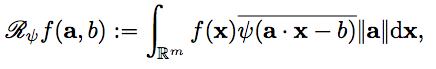
を得ます.そして,Ψとηが許容条件
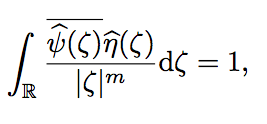
を満たす時,fに対して次のような再生公式が成り立ちます.
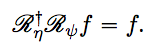
得られた再生公式を離散化することにより,活性化関数ηを用いたニューラルネットの近似性能を検証することができるとされています.
ReLUネットワークへの拡張
先の方法は活性化関数ηが有界関数(sigmoid関数やtanh関数)を用いた場合でのリッジレット変換であり, ReLUのような非有界関数を扱うことは想定されていませんでした.そこでSonodaらはアイデアを拡張して,活性化関数ηがReLUのような非有界かつLizorkin超関数に属するクラスであっても,ReLUネットワークを積分表現で分析できることを示しました.ReLUネットワークの万能近似性能については,フーリエスライス定理,ラドン変換,パーセバルの定理を用いた3つの再生公式によって,それを満たすことが示されています.そして,ニューラルネットが学習の結果として獲得する情報表現の正体はリッジレット変換であると述べています.
この論文の非常に興味深い主張として,許容条件に従えば,リッジレット変換を単純に離散化することによって,誤差逆伝播を経たずにネットワークを学習させることが可能であるということです.また,この理論を応用することでランダム初期化よりも有利な条件で学習させる方法も示しています[9].
深層学習への応用
深層学習の積分表現は自明ではないらしく,論文は投稿の最中ということなので,公開を待つことにします.
おわりに
ニューラルネットの解析は私が強く興味を持っている研究の一つなので,今回取り上げた論文はとても面白く感じました. 私の理解が足りてない部分が多々あるので,それぞれの要素や論文についても時間が取れたら書きたいところです.
参考文献
[1] Irie and Miyake. Capabilities of three-layered Perceptrons. In Proceedings of International Conference on Neural Networks. pp. 641-648 (1988).
[2] Cybenko. Approximation by superpositions of a sigmoid function. Mathematics of Control, Signals and Systems, pp. 303-314 (1989).
[3] White H. Connectionist nonparametric regression: multilayer feedforward networks can learn arbitrary mappings. Neural Networks. pp. 535-
549 (1990).
[4] Funahashi. On the approximate realization of continuous mappings by neural networks. Neural Networks. pp. 183-192 (1989).
[5] Girosi and Anzellotti. Convergence rates of approximation by translates (Tech. Rep. A.I. memo 1288). Articial Intelligence Laboratory, Massachusetts Institute of Technology (1992).
[6] Noboru Murata. An Integral representation of functions using three-layered networks and their approximation bounds. Neural Networks, Vol. 9, No. 6, pp. 947–956 (1996).
[7] Cands, E. J. Harmonic analysis of neural networks, Appl. Comput. Harmon. Anal. 6, pp. 197-218 (1999).
[8] Sho Sonoda, Noboru Murata. Neural network with unbounded activation functions is universal approximator. Appl. Comput. Harmon. Anal (2015).
[9] Sho Sonoda and Noboru Murata. Sampling hidden parameters from oracle distribution. In 24th Int. Conf. Artif. Neural Networks, Vol. 8681, pp. 539–546 (2014).